基于policy gradient的强化学习方法的梳理总结,从经典的策略梯度算法开始,讨论A3C,DDPG,PPO,以及IMPALA等系列算法的基本思想和实现。
Policy Gradient 算法 在展开策略梯度之前,先回顾两个概念,确定性策略和随机策略。确定性策略是指在相同的状态下,其输出的动作是确定的,可使用 π ( s ) \pi(s) π ( s ) π ( a ∣ s ) \pi(a|s) π ( a ∣ s )
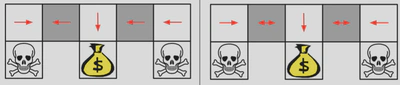
上面左图是一个确定性策略的例子[4],在游戏中,智能体分不清两个灰色格子的区别,因为左右两边都是白色的,那么这个策略就不是一个好的策略,如果起始位置在第一个白格子处,智能体就会出现死循环;上右图是一个随机策略的例子,在灰色格子,具有一定的概率向左或者向右走,那么智能体在任何位置开始,最终都会可以到达目标位置。
前文讲到的DQN,Value Based,强化学习方法在很多领域都得到比较好的应用,但是Value Based强化学习方法也有一些局限性,主要包括:
值函数求解最优策略的时候,需要求解 arg max a Q θ ( s , a ) \scriptsize \arg \max_a Q_\theta (s,a) arg max a Q θ ( s , a ) 对受限状态下的问题处理能力不足。在使用特征来描述状态空间中的某一个状态时,有可能因为个体观测的限制(部分观测)或者建模的局限,导致真实环境下本来不同的两个状态,在我们的建模状态空间却是一样的,进而很有可能导致value Based方法无法得到最优解[5]。 无法解决随机策略问题。Value Based强化学习方法对应的最优策略通常是确定性策略,因为它是从众多行为中选择一个最大价值的行为,而有些问题的最优策略却是随机策略,这种情况下同样是无法通过基于价值的学习来求解的。如上面提到的例子所示。 那么Policy Based的强化学习方法在这些问题上又具有哪些优势呢?
首先, 我们从policy-based方法的定义出发。基于采样的方式,我们把策略形式为:π θ ( s , a ) = P ( a │ s ; θ ) ≈ π ( a ∣ s ) \scriptsize \pi_\theta (s,a) = P(a│s;\theta) \approx \pi(a|s) π θ ( s , a ) = P ( a │ s ; θ ) ≈ π ( a ∣ s ) π \pi π θ \theta θ
我们把优化的目标表示为初始状态收获的期望,策略 π \pi π θ \theta θ π ( s , a ) \pi(s,a) π ( s , a ) π ( s , a ; θ ) , π = π ( θ ) \pi(s,a; \theta),\pi=\pi(\theta) π ( s , a ; θ ) , π = π ( θ )
J 1 ( θ ) = V π ( θ ) ( s 1 ) = E π ( θ ) ( G 1 ) = E π ( G 1 )
\scriptsize
J_1 (\theta) = V_{\pi (\theta)} (s_1) = \mathbb{E}_{\pi (\theta)} (G_1) = \mathbb{E}_\pi (G_1)
J 1 ( θ ) = V π ( θ ) ( s 1 ) = E π ( θ ) ( G 1 ) = E π ( G 1 ) 在连续状态的环境中,我们的优化目标也可以定义为平均价值
J a v V ( θ ) = ∑ s d π ( s ) V π ( s )
\scriptsize
J_{av} V(\theta) = \sum_{s} d_\pi (s) V_\pi (s)
J a v V ( θ ) = s ∑ d π ( s ) V π ( s ) 其中,d π ( s ) = ∑ t = 0 ∞ γ t Pr { s t = s ∣ s 0 , π } \scriptsize d_\pi (s) = \sum_{t=0}^{\infty} \gamma^t \Pr \{ s_t = s \mid s_0, \pi \} d π ( s ) = ∑ t = 0 ∞ γ t Pr { s t = s ∣ s 0 , π } π ( θ ) \pi(\theta) π ( θ ) γ \gamma γ
同样在episodic 任务中,我们可以定义每一个time step 的平均奖励, 即
J a v R ( θ ) = lim n → ∞ ( 1 n E { ∑ i = 1 n r i ∣ π } ) = ∑ s d π ( s ) ∑ a π ( s , a ) R s a
\scriptsize
\begin{align*}
J_{av} R(\theta) &= \lim_{n \to \infty} \left( \frac{1}{n} \mathbb{E} \left\{ \sum_{i=1}^{n} r_i \mid \pi \right\} \right) = \sum_{s} d_\pi (s) \sum_{a} \pi(s, a) R_s^a
\end{align*}
J a v R ( θ ) = n → ∞ lim ( n 1 E { i = 1 ∑ n r i ∣ π } ) = s ∑ d π ( s ) a ∑ π ( s , a ) R s a 其中,d π ( s ) = lim t → ∞ Pr { s t = s ∣ s 0 , π } \scriptsize d_\pi (s) = \lim_{t \to \infty} \Pr \{ s_t = s \mid s_0, \pi \} d π ( s ) = lim t → ∞ Pr { s t = s ∣ s 0 , π } s 0 s_0 s 0 π \pi π s t s_t s t
无论使用哪个优化目标,我们都是需要找到最大化 J ( θ ) J(\theta) J ( θ ) θ \theta θ θ \theta θ
使用状态分布表示的策略梯度:
∇ θ J ( θ ) = ∂ J ∂ θ = ∑ s d π ( s ) ∑ a ∂ π ( s , a ) ∂ θ Q π ( s , a )
\scriptsize
\nabla_\theta J(\theta) = \frac{\partial J}{\partial \theta} = \sum_{s} d_\pi (s) \sum_{a} \frac{\partial \pi(s,a)}{\partial \theta} Q^\pi(s,a)
∇ θ J ( θ ) = ∂ θ ∂ J = s ∑ d π ( s ) a ∑ ∂ θ ∂ π ( s , a ) Q π ( s , a ) 使用期望方式表示策略梯度:
∇ θ J ( θ ) = E π θ [ ∇ θ log π θ ( s , a ) Q π ( s , a ) ]
\scriptsize
\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta} \left[ \nabla_\theta \log \pi_\theta(s, a) Q^\pi (s, a) \right]
∇ θ J ( θ ) = E π θ [ ∇ θ log π θ ( s , a ) Q π ( s , a ) ] 这个也称之为策略梯度定理(Policy Gradient Theorem)。为了便于编程实现,我们再次从似然性的角度来推导,即
定义状态-动作序列(轨迹):τ = { s 0 , a 0 , s 1 , a 1 , … , s T , a T } \scriptsize \tau = \{s_0, a_0, s_1, a_1, \ldots, s_T, a_T \} τ = { s 0 , a 0 , s 1 , a 1 , … , s T , a T }
轨迹τ \tau τ R ( τ ) = ∑ t = 0 T R ( s t , a t ) \scriptsize R(\tau) = \sum_{t=0}^{T} R(s_t, a_t) R ( τ ) = ∑ t = 0 T R ( s t , a t )
轨迹τ \tau τ p θ ( τ ) = p ( s 1 ) ∏ t = 1 T p θ ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) \scriptsize p_\theta(\tau) = p(s_1) \prod_{t=1}^{T} p_\theta(a_t \mid s_t) p(s_{t+1} \mid s_t, a_t) p θ ( τ ) = p ( s 1 ) ∏ t = 1 T p θ ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t )
那么强化学习的优化目标可以表示为:
R ‾ θ = ∑ τ R ( τ ) p θ ( τ ) = E τ ∼ p θ ( τ ) [ R ( τ ) ]
\scriptsize
\overline{R}_\theta = \sum_{\tau} R(\tau) p_\theta(\tau) = \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau)]
R θ = τ ∑ R ( τ ) p θ ( τ ) = E τ ∼ p θ ( τ ) [ R ( τ )] 根据公式:∇ log f ( x ) = 1 f ( x ) ∇ f ( x ) \scriptsize \nabla \log f(x) = \frac{1}{f(x)} \nabla f(x) ∇ log f ( x ) = f ( x ) 1 ∇ f ( x )
∇ R ‾ θ = ∑ τ R ( τ ) ∇ p θ ( τ ) = ∑ τ R ( τ ) p θ ( τ ) ∇ p θ ( τ ) p θ ( τ ) = ∑ τ R ( τ ) p θ ( τ ) ∇ log p θ ( τ ) = E τ ∼ p θ ( τ ) [ R ( τ ) ∇ log p θ ( τ ) ]
\scriptsize
\begin{align*}
\nabla \overline{R}_\theta &= \sum_{\tau} R(\tau) \nabla p_\theta(\tau) \\
&= \sum_{\tau} R(\tau) p_\theta(\tau) \frac{\nabla p_\theta(\tau)}{p_\theta(\tau)} \\
&= \sum_{\tau} R(\tau) p_\theta(\tau) \nabla \log p_\theta(\tau) \\
&= \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla \log p_\theta(\tau)]
\end{align*}
∇ R θ = τ ∑ R ( τ ) ∇ p θ ( τ ) = τ ∑ R ( τ ) p θ ( τ ) p θ ( τ ) ∇ p θ ( τ ) = τ ∑ R ( τ ) p θ ( τ ) ∇ log p θ ( τ ) = E τ ∼ p θ ( τ ) [ R ( τ ) ∇ log p θ ( τ )] 最终策略梯度变成了求R ( τ ) ∇ log p θ ( τ ) \scriptsize R(\tau) \nabla \log p_\theta(\tau) R ( τ ) ∇ log p θ ( τ ) π θ \pi_\theta π θ τ \tau τ
∇ R ‾ θ = E τ ∼ p θ ( τ ) [ R ( τ ) ∇ log p θ ( τ ) ] ≈ 1 N ∑ n = 1 N R ( τ n ) ∇ log p θ ( τ n ) = 1 N ∑ n = 1 N ∑ t = 1 T n R ( τ n ) ∇ log p θ ( a t n ∣ s t n )
\scriptsize
\begin{align*}
\nabla \overline{R}_\theta &= \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla \log p_\theta(\tau)] \approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) \nabla \log p_\theta (\tau^n) \\
&= \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} R(\tau^n) \nabla \log p_\theta (a_t^n \mid s_t^n)
\end{align*}
∇ R θ = E τ ∼ p θ ( τ ) [ R ( τ ) ∇ log p θ ( τ )] ≈ N 1 n = 1 ∑ N R ( τ n ) ∇ log p θ ( τ n ) = N 1 n = 1 ∑ N t = 1 ∑ T n R ( τ n ) ∇ log p θ ( a t n ∣ s t n ) 在实际实验中,假设 τ n \tau^n τ n T n T_n T n R ( τ ) = ∑ t = 0 T r t \scriptsize R(\tau) = \sum_{t=0}^{T} r_t R ( τ ) = ∑ t = 0 T r t ∇ log p θ ( τ n ) \scriptsize \nabla \log p_\theta (\tau^n) ∇ log p θ ( τ n ) τ \tau τ θ \theta θ
R ( τ n ) \scriptsize R(\tau^n ) R ( τ n ) R ( τ n ) \scriptsize R(\tau^n ) R ( τ n ) R ( τ n ) \scriptsize R(\tau^n ) R ( τ n )
以上即为策略梯度方法的核心内容。
A3C 算法 Actor-Critic 方法 在介绍A2c之前,我们先回顾Actor-Critic,AC方法。我们可以把该方法类比为:行动者在表演的时候有评论家指点。这样行动者就会表演得越来越好;同时,评论家也在不断进步,即评论者对行动者动作评价地更加准确,共同进步,使得目标策略越来越好。具体来说,AC方法是一种结合了Policy Gradient (Actor) 和 Function Approximation (Critic) 的方法. Actor 基于概率选择行为, Critic 基于 Actor 的行为评判该行为的得分, 然后,Actor 再根据 Critic 的评分(比如TD error)更新行为选择的概率。
这时我们回过头看看前面的策略梯度表示,∇ R ˉ θ = E τ ∼ p θ ( τ ) [ R ( τ ) ∇ log p θ ( τ ) ] \scriptsize \nabla \bar{R}_{\theta} = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [R(\tau) \nabla \log p_{\theta}(\tau)] ∇ R ˉ θ = E τ ∼ p θ ( τ ) [ R ( τ ) ∇ log p θ ( τ )]
∇ R ˉ θ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n R ( τ n ) ∇ log p θ ( a t n ∣ s t n )
\scriptsize \nabla \bar{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \textcolor{red}{R(\tau^n)} \nabla \log p_{\theta} (a_t^n | s_t^n)
∇ R ˉ θ ≈ N 1 n = 1 ∑ N t = 1 ∑ T n R ( τ n ) ∇ log p θ ( a t n ∣ s t n ) 那么,AC方法中Actor参数的梯度可以表示为:
∇ R ˉ θ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n Q π θ ( s t n , a t n ) ∇ log p θ ( a t n ∣ s t n )
\scriptsize \nabla \bar{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \textcolor{red}{Q^{\pi_{\theta}} (s_t^n, a_t^n)} \nabla \log p_{\theta} (a_t^n | s_t^n)
∇ R ˉ θ ≈ N 1 n = 1 ∑ N t = 1 ∑ T n Q π θ ( s t n , a t n ) ∇ log p θ ( a t n ∣ s t n ) 此时,Critic根据估计的Q值和实际Q值得平方误差进行采样更新,其loss可以表示为,
L ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( r t n + max a t + 1 n Q π θ ( s t + 1 n , a t + 1 n ) − Q π θ ( s t n , a t n ) ) 2
\scriptsize L \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \left( r_t^n + \max_{a_{t+1}^n} Q^{\pi_{\theta}} (s_{t+1}^n, a_{t+1}^n) - Q^{\pi_{\theta}} (s_t^n, a_t^n) \right)^2
L ≈ N 1 n = 1 ∑ N t = 1 ∑ T n ( r t n + a t + 1 n max Q π θ ( s t + 1 n , a t + 1 n ) − Q π θ ( s t n , a t n ) ) 2 以上即为AC方法的主要内容。
A2C 方法 现在,我们再次回到策略梯度的角度进行分析。
策略梯度使用采样的方式进行迭代,在实际的场景中可能会出现这样的一些问题:reward的期望可能永远都是正值,那么某些没有被采样到的,本质上是好的轨迹,可能会被进行过多次采样的其他轨迹“淹没”了。
这时我们可以把reward 增加一个基准偏置b,使得反馈量包含正负两种数值来解决这个问题。这个值得大小一般可以使用reward 的期望值表示,即 b ≈ ∑ [ R ( τ ) ] \scriptsize b≈\sum[R(\tau)] b ≈ ∑ [ R ( τ )]
∇ R θ ˉ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( R ( τ n ) − b ) ∇ log p θ ( a t n ∣ s t n )
\scriptsize
\nabla R_{\bar{\theta}} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \left( R(\tau^{n}) - \textcolor{red}{b} \right) \nabla \log p_{\theta} \left( a_t^n \mid s_t^n \right)
∇ R θ ˉ ≈ N 1 n = 1 ∑ N t = 1 ∑ T n ( R ( τ n ) − b ) ∇ log p θ ( a t n ∣ s t n ) AC方法下的策略梯度可以表示为
∇ R θ ˉ ≈ 1 N ∑ n = 1 N ( ∑ t = 1 T n ( Q π θ ( s t n , a t n ) − b ) ∇ log p θ ( a t n ∣ s t n ) )
\scriptsize
\nabla R_{\bar{\theta}} \approx \frac{1}{N} \sum_{n=1}^{N} \left( \sum_{t=1}^{T_n} \left( Q^{\pi_{\theta}} (s_t^n, a_t^n) - \textcolor{red}{b} \right) \nabla \log p_{\theta} \left( a_t^n \mid s_t^n \right) \right)
∇ R θ ˉ ≈ N 1 n = 1 ∑ N ( t = 1 ∑ T n ( Q π θ ( s t n , a t n ) − b ) ∇ log p θ ( a t n ∣ s t n ) ) 这时我们再次观察 Q π θ ( s t n , a t n ) \scriptsize Q^{\pi_{\theta}} (s_t^n, a_t^n) Q π θ ( s t n , a t n ) R ( τ ) \scriptsize R(\tau) R ( τ ) R ( τ ) = ∑ t = 1 T r t \scriptsize R(\tau) = \sum_{t=1}^{T} r_t R ( τ ) = ∑ t = 1 T r t 动作之后 接收到的reward值,即∑ t ′ = t T n r t ′ n \scriptsize \sum_{t'=t}^{T_n} r_{t'}^n ∑ t ′ = t T n r t ′ n ∑ t ′ = t T n γ t ′ − t r t ′ n \scriptsize \sum_{t'=t}^{T_n} \gamma^{t'-t} r_{t'}^n ∑ t ′ = t T n γ t ′ − t r t ′ n
∇ R θ ˉ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( ∑ t ′ = t T n γ t ′ − t r t ′ n − b ) ∇ log p θ ( a t n ∣ s t n )
\scriptsize
\nabla R_{\bar{\theta}} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} (\sum_{t'=t}^{T_n} \gamma^{t'-t} r_{t'}^n - b ) \nabla \log p_{\theta} ( a_t^n \mid s_t^n )
∇ R θ ˉ ≈ N 1 n = 1 ∑ N t = 1 ∑ T n ( t ′ = t ∑ T n γ t ′ − t r t ′ n − b ) ∇ log p θ ( a t n ∣ s t n ) 那么实际上,我们从Q函数的定义看:Q π ( s , a ) \scriptsize Q_\pi (s,a) Q π ( s , a ) π \scriptsize \pi π
现在,我们把基准偏置b表示为,状态的价值函数,V π θ ( s t n ) \scriptsize V^{\pi_{\theta}} (s_t^n) V π θ ( s t n )
∇ R θ ˉ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( Q π θ ( s t n , a t n ) − V π θ ( s t n ) ) ∇ log p θ ( a t n ∣ s t n )
\scriptsize
\nabla R_{\bar{\theta}} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} ( Q^{\pi_{\theta}} (s_t^n, a_t^n) - V^{\pi_{\theta}} (s_t^n) ) \nabla \log p_{\theta} ( a_t^n \mid s_t^n )
∇ R θ ˉ ≈ N 1 n = 1 ∑ N t = 1 ∑ T n ( Q π θ ( s t n , a t n ) − V π θ ( s t n )) ∇ log p θ ( a t n ∣ s t n ) 这时,我们需要分别计算两个网络:状态-动作值函数Q π θ \scriptsize Q^{\pi_{\theta}} Q π θ V π θ \scriptsize V^{\pi_{\theta}} V π θ
∇ R θ ˉ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( r t n + V π ( s t + 1 n ) − V π ( s t n ) ) ∇ log p θ ( a t n ∣ s t n )
\scriptsize
\nabla R_{\bar{\theta}} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} ( r_t^n + V^{\pi} (s_{t+1}^n) - V^{\pi} (s_t^n) ) \nabla \log p_{\theta} ( a_t^n \mid s_t^n )
∇ R θ ˉ ≈ N 1 n = 1 ∑ N t = 1 ∑ T n ( r t n + V π ( s t + 1 n ) − V π ( s t n )) ∇ log p θ ( a t n ∣ s t n ) 这样会增加一定的方差,不过可以忽略不计,这样我们就得到了Advantage Actor-Critic, A2C方法[9],此时的Critic变为估计状态价值V的网络。因此Critic网络的loss可以表示为:
loss ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( r t n + V π ( s t + 1 n ) − V π ( s t n ) ) 2
\scriptsize
\text{loss} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} ( r_t^n + V^{\pi} (s_{t+1}^n) - V^{\pi} (s_t^n) ) ^2
loss ≈ N 1 n = 1 ∑ N t = 1 ∑ T n ( r t n + V π ( s t + 1 n ) − V π ( s t n ) ) 2 我们再解释下为什么叫Advantage AC方法。这时,我们引入一个优势函数的概念,Advantage function,来表示:在状态s t \scriptsize s_t s t a t \scriptsize a_t a t A ( s , a ) = Q ( s , a ) − V ( s ) \scriptsize A(s,a) = Q(s,a) - V(s) A ( s , a ) = Q ( s , a ) − V ( s ) Q ( s , a ) \scriptsize Q(s,a) Q ( s , a ) V ( s ) \scriptsize V(s) V ( s )
以上即为A2C方法的内容。具体基于Advantage继续优化的方法,我们留到PPO章节再做分析。
A3C 方法 我们知道,直接更新策略的方法,其迭代速度往往都是非常慢的,为了充分利用计算资源,又有了Asynchronous Advantage Actor-Critic,A3C方法[10-12]。
A3C架构,包含一个主网络和多个Worker,每一个Worker可以看做是一个A2C的net,A3C主要有两个操作:pull和push。
pull:把主网络的参数直接赋予Worker中的网络 push:使用各Worker中的梯度,对主网络的参数进行更新 相比DQN算法,A3C算法不需要使用经验池来存储历史样本,并随机抽取来克服样本的相关性,节约了存储空间,并且采用异步训练,大大加倍了数据的采样速度,因此也提升了训练速度。
DDPG 在讲DDPG之前,我们免不了先从Deterministic policy gradient (DPG)[13]开始,实际上,其较完整的发展路线是:off-policy P G → D P G → D D P G \scriptsize \text{off-policy} PG → DPG → DDPG off-policy PG → D PG → DD PG
Off-Policy PG Off-Policy的行为策略和目标策略是两个不同的策略,那么它带来的好处就是:
目标策略更新的时候,不需要等到行为策略完成一个完整的episode。那么就可以使用比如experience replay 类似的机制来重复使用过去的经验数据,进而提高数据的采样效率; 目标策略和行为策略是两个不同的策略,可以更好地探索。 现在,我们引入一个新的行为策略,用来采集数据,记为 β ( a ∣ s ) \scriptsize \beta(a|s) β ( a ∣ s )
J ( θ ) = ∑ s ∈ S d β ( s ) ∑ a ∈ A Q π ( s , a ) π θ ( a ∣ s ) = E s ∼ d β [ ∑ a ∈ A Q π ( s , a ) π θ ( a ∣ s ) ]
\scriptsize
\begin{align*}
J(\theta) &= \sum_{s\in S}\ d^{\beta}(s) \sum_{a\in A} Q^{\pi}(s,a) \pi_{\theta}(a|s) \\
&= \mathbb{E}_{s \sim d^{\beta}} \left[ \sum_{a \in A} Q^{\pi}(s,a) \pi_{\theta}(a \mid s) \right]
\end{align*}
J ( θ ) = s ∈ S ∑ d β ( s ) a ∈ A ∑ Q π ( s , a ) π θ ( a ∣ s ) = E s ∼ d β [ a ∈ A ∑ Q π ( s , a ) π θ ( a ∣ s ) ] d β ( s ) \scriptsize d^{\beta}(s) d β ( s ) β \scriptsize \beta β d β ( s ) = lim t → ∞ P ( S t = s ∣ S 0 , β ) \scriptsize d^{\beta}(s)=\lim_{t \to \infty} P(S_t = s \mid S_0, \beta) d β ( s ) = lim t → ∞ P ( S t = s ∣ S 0 , β ) Q π \scriptsize Q^{\pi} Q π π \scriptsize \pi π ∇ θ J ( θ ) = E π θ [ ∇ θ log π θ ( s , a ) Q π ( s , a ) ] \scriptsize \nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}} \left[ \nabla_{\theta} \log \pi_{\theta}(s,a) Q^{\pi}(s,a) \right] ∇ θ J ( θ ) = E π θ [ ∇ θ log π θ ( s , a ) Q π ( s , a ) ] β ( a ∣ s ) \scriptsize \beta(a|s) β ( a ∣ s )
∇ θ J β ( θ ) = E β [ π θ ( a ∣ s ) β ( a ∣ s ) Q π ( s , a ) ∇ θ log π θ ( a ∣ s ) ]
\scriptsize
\nabla_{\theta} J_{\beta} (\theta) = \mathbb{E}_{\beta} \left[ \frac{\pi_{\theta}(a|s)}{\beta(a|s)} Q^{\pi}(s,a) \nabla_{\theta} \log \pi_{\theta}(a|s) \right]
∇ θ J β ( θ ) = E β [ β ( a ∣ s ) π θ ( a ∣ s ) Q π ( s , a ) ∇ θ log π θ ( a ∣ s ) ] π θ ( a ∣ s ) β ( a ∣ s ) \scriptsize \frac{\pi_{\theta}(a|s)}{\beta(a|s)} β ( a ∣ s ) π θ ( a ∣ s )
E x ∼ p [ f ( x ) ] = ∫ f ( x ) p ( x ) d x = ∫ f ( x ) p ( x ) q ( x ) q ( x ) d x = E x ∼ q [ f ( x ) p ( x ) q ( x ) ]
\scriptsize
\begin{align*}
\mathbb{E}_{x\sim \textcolor{red}{p}}[f(x)] &= \int f(x)p(x)dx = \int f(x) \frac{p(x)}{q(x)} q(x)dx \\
&= \mathbb{E}_{x \sim \textcolor{red}{q}}\left[ f(x) \textcolor{red}{\frac{p(x)}{q(x)}} \right]
\end{align*}
E x ∼ p [ f ( x )] = ∫ f ( x ) p ( x ) d x = ∫ f ( x ) q ( x ) p ( x ) q ( x ) d x = E x ∼ q [ f ( x ) q ( x ) p ( x ) ] w ( x ) = p ( x ) / q ( x ) \scriptsize w(x)= p(x)/q(x) w ( x ) = p ( x ) / q ( x ) ∑ x ∼ p [ f ( x ) ] \scriptsize \sum_{x \sim p} [f(x)] ∑ x ∼ p [ f ( x )] q ( x ) \scriptsize q(x) q ( x )
DPG (确定性策略梯度) 那么,我们继续回到DPG,先回顾下前面推导的随机策略梯度计算表达式,
∇ θ J ( θ ) = E π θ [ ∇ θ log π θ ( s , a ) Q π ( s , a ) ] = E s ∼ ρ π , a ∼ π θ [ ∇ θ log π θ ( s , a ) Q π ( s , a ) ]
\scriptsize
\begin{align*}
\nabla_{\theta} J(\theta) &= \mathbb{E}_{\pi_{\theta}} \left[ \nabla_{\theta} \log \pi_{\theta}(s, a) Q^{\pi}(s, a) \right] \\
&= \mathbb{E}_{s \sim \rho^{\pi}, \, a \sim \pi_{\theta}} \left[ \nabla_{\theta} \log \pi_{\theta}(s, a) Q^{\pi}(s, a) \right]
\end{align*}
∇ θ J ( θ ) = E π θ [ ∇ θ log π θ ( s , a ) Q π ( s , a ) ] = E s ∼ ρ π , a ∼ π θ [ ∇ θ log π θ ( s , a ) Q π ( s , a ) ] 可以看到,以上的策略梯度公式是关于状态和动作的期望,在求期望时,需要同时对状态分布和动作分布求积分,这就要求在状态空间和动作空间采集⼤量的样本,这样求均值才能近似期望。
然⽽确定性策略(deterministic policy)的动作是确定的,即 a = π ( s ) \scriptsize a = \pi(s) a = π ( s )
∇ θ J ( π θ ) = E s ∼ ρ π [ ∇ θ π θ ( s , a ) ⋅ ∇ a Q π ( s , a ) ∣ a = π θ ( s ) ]
\scriptsize
\nabla_{\theta} J(\pi_{\theta}) = \mathbb{E}_{\textcolor{red}{s \sim \rho^{\pi}}} \left[ \nabla_{\theta} \pi_{\theta}(s, \textcolor{red}{a}) \cdot \nabla_{a} Q^{\pi}(s, a) \big|_{a = \pi_{\theta}(s)} \right]
∇ θ J ( π θ ) = E s ∼ ρ π [ ∇ θ π θ ( s , a ) ⋅ ∇ a Q π ( s , a ) a = π θ ( s ) ] 跟随机策略梯度的式子相比,少了对动作的积分,多了回报Q函数对动作的导数。具体推导过程可以详见DPG的论文[13],证明了DPG是之前随机策略梯度定理当policy的variance趋向于0时的极限,具体推导这里暂不展开。
DPG的求解不需要在动作空间采样积分。相⽐于随机策略⽅法,DPG需要的样本数据更⼩。尤其是对那些动作空间很⼤的智能体(⽐如多关节机器⼈),由于动作空间维数很⼤,如果⽤随机策略,需要在这些动作空间中⼤量采样。通常来说,确定性策略⽅法的效率⽐随机策略的效率⾼⼗倍,这也是确定性策略⽅法最主要的优点[7]。当然,相⽐于确定性策略,随机策略也有其自身的优点:它可以将探索和改善集成到同⼀个策略中。
如果使用确定性策略方法,Agent与环境的交互过程是固定的,即基于某一状态下,策略提供的行为选择总是为固定的一个。那么,我们需要怎么进行环境的探索呢?当然,前面提到的AC方法为我们提供了解决思路,使用一个Actor网络进行随机策略探索,而评估策略使用确定性策略即可。基于on-policy的一个AC计算的过程示例如下[14]:
基于SARSA的TD error: δ t = R t + γ Q w ( s t + 1 , a t + 1 ) − Q w ( s t , a t ) \scriptsize \delta_t = R_t + \gamma Q_w(s_{t+1}, a_{t+1}) - Q_w(s_t, a_t) δ t = R t + γ Q w ( s t + 1 , a t + 1 ) − Q w ( s t , a t )
基于TD error 更新: w t + 1 = w t + α w δ t ∇ w Q w ( s t , a t ) \scriptsize w_{t+1} = w_t + \alpha_w \delta_t \nabla_w Q_w(s_t, a_t) w t + 1 = w t + α w δ t ∇ w Q w ( s t , a t )
确定性策略定理: θ t + 1 = θ t + α θ ∇ a Q w ( s t , a t ) ∇ θ μ θ ( s ) ∣ a = μ θ ( s ) \scriptsize \theta_{t+1} = \theta_t + \alpha_{\theta} \nabla_a Q_w(s_t, a_t) \nabla_{\theta} \mu_{\theta}(s) \big|_{a = \mu_{\theta}(s)} θ t + 1 = θ t + α θ ∇ a Q w ( s t , a t ) ∇ θ μ θ ( s ) a = μ θ ( s )
由于我们使用了确定性策略,除非环境中有大量的噪声,不然上面的探索过程,仍然还是很难收敛。那么我们是否可以手动引入噪声,(使之非确定性化),用于辅助探索呢?
实际上,我们可以使用上一章节描述的off-policy Policy Gradient机制来实现辅助探索。那么我们基于重要性采样的公式,可以得到off-policy下的确定策略梯度计算表达式,
∇ θ J β ( π θ ) = E s ∼ ρ β [ ∇ θ μ θ ( s , a ) ∇ a Q μ ( s , a ) ∣ a = μ θ ( s ) ] = E s ∼ ρ β [ ∇ θ μ θ ( s ) ∇ a Q μ ( s , a ) ∣ a = μ θ ( s ) ]
\scriptsize
\begin{align*}
\nabla_{\theta} J_{\textcolor{red}{\beta}} (\pi_{\theta}) &= \mathbb{E}_{s \sim \rho^{\beta}} \left[ \nabla_{\theta} \mu_{\theta}(s, \textcolor{red}{\sout{a}}) \nabla_a Q^{\mu}(s,a) \big|_{a = \mu_{\theta}(s)} \right] \\
&= \mathbb{E}_{s \sim \rho^{\beta}} \left[ \nabla_{\theta} \mu_{\theta}(s) \nabla_a Q^{\mu}(s,a) \big|_{a = \mu_{\theta}(s)} \right]
\end{align*}
∇ θ J β ( π θ ) = E s ∼ ρ β [ ∇ θ μ θ ( s , a ) ∇ a Q μ ( s , a ) a = μ θ ( s ) ] = E s ∼ ρ β [ ∇ θ μ θ ( s ) ∇ a Q μ ( s , a ) a = μ θ ( s ) ] 实际上,由于重要性采样使用简单的概率分布去估计复杂的概率分布,而确定性概率的动作是确定值,而不是概率分布,故确定性策略梯度求解的时候,将这项重要性权重也去掉了。
注意公式中 μ \scriptsize \mu μ π \scriptsize \pi π
DDPG DeepMind 在2016年提出Deep Deterministic Policy Gradient,DDPG[15],将深度神经网络与DPG相结合,用于处理连续动作问题。在 DQN的: 1)经验回放和2)独立的目标网络这点优化技巧的基础上,DDPG算法: 3)采用 AC 架构;4)策略网络采用 DPG 更新,利用策略梯度方法直接优化用深度神经网络参数化表示的 policy,即网络的输出就是动作。即得到了我们的DDPG算法。所谓深度,是指利用深度神经网络逼近行为值函数Q w ( s , a ) \scriptsize Q^w (s,a) Q w ( s , a ) μ θ ( s ) \scriptsize \mu_\theta (s) μ θ ( s )
为了进一步提高探索的效率,在动作输出上面,再次增加一个noise N \scriptsize N N
μ ′ ( s ) = μ θ ( s ) + N
\scriptsize \mu'(s) = \mu_\theta(s) + N
μ ′ ( s ) = μ θ ( s ) + N 另外,DDPG在Actor和Critic参数的更新上均使用软更新,soft update,类似信息领域的“低通滤波”。即 τ ≪ 1 : θ ′ ← τ θ + ( 1 − τ ) θ ′ \scriptsize \tau \ll 1: \quad \theta' \leftarrow \tau \theta + (1 - \tau) \theta' τ ≪ 1 : θ ′ ← τ θ + ( 1 − τ ) θ ′
PPO Proximal Policy Optimization Algorithms[16],PPO算法是OpenAI于2017年公布的一个基于策略梯度的方法,由于其易用性和优异的性能表现特性,很快即成为OpenAI的默认强化学习算法[17]。
我们首先回顾下,前面推导的基于AC的策略梯度的计算表达式:
∇ R ˉ θ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( ∑ t ′ = t T n γ t ′ − t r t ′ n − b ) ∇ log p θ ( a t n ∣ s t n )
\scriptsize
\nabla \bar{R}_\theta \approx \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} \left( \sum_{t'=t}^{T_n} \gamma^{t'-t} r_{t'}^n - b \right) \nabla \log p_\theta (a_t^n | s_t^n)
∇ R ˉ θ ≈ N 1 n = 1 ∑ N t = 1 ∑ T n ( t ′ = t ∑ T n γ t ′ − t r t ′ n − b ) ∇ log p θ ( a t n ∣ s t n ) 这是一个on-policy的计算过程,前面提到的A3C,通过多个A2C的net异步化,来实现的训练的提速。
那么是否可以从off-policy的角度来解决这个问题呢?
我们还得回顾一下,前面提到的优势函数的定义,∑ t = 1 T n ( ∑ t ′ = t T n γ t ′ − t r t ′ n − b ) \scriptsize \sum_{t=1}^{T_n} \left( \sum_{t'=t}^{T_n} \gamma^{t'-t} r_{t'}^n - b \right) ∑ t = 1 T n ( ∑ t ′ = t T n γ t ′ − t r t ′ n − b ) A θ ( s t , a t ) \scriptsize A^\theta (s_t,a_t) A θ ( s t , a t )
OpenAI给出的答案是,可以的。但是需要有一定的条件限制的。
我们先继续基于优势函数的推导。
根据前面推导的重要性采样法则: E x ∼ p [ f ( x ) ] = E x ∼ q [ f ( x ) p ( x ) q ( x ) ] \scriptsize E_{x \sim p}[f(x)] = E_{x \sim q}\left[f(x) \frac{p(x)}{q(x)} \right] E x ∼ p [ f ( x )] = E x ∼ q [ f ( x ) q ( x ) p ( x ) ]
我们可以把前面的策略梯度的更新过程off-policy化。即用策略π θ ′ \scriptsize \pi_{\theta'} π θ ′ π θ \scriptsize \pi_{\theta} π θ
∇ R θ = E ( s t , a t ) ∼ π θ [ A θ ( s t , a t ) ∇ log p θ ( a t ∣ s t ) ] = E ( s t , a t ) ∼ π θ ′ [ p θ ( s t , a t ) p θ ′ ( s t , a t ) A θ ( s t , a t ) ∇ log p θ ( a t ∣ s t ) ] = E ( s t , a t ) ∼ π θ ′ [ p θ ( a t ∣ s t ) p θ ( s t ) p θ ′ ( a t ∣ s t ) p θ ′ ( s t ) A θ ′ ( s t , a t ) ∇ log p θ ( a t ∣ s t ) ] = E ( s t , a t ) ∼ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ∇ log p θ ( a t ∣ s t ) ]
\scriptsize
\begin{align*}
\scriptsize \nabla R_\theta &= E_{(s_t, a_t) \sim \pi_\theta} \left[ A^\theta(s_t, a_t) \nabla \log p_\theta(a_t | s_t) \right] \\
&= E_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \frac{p_\theta(s_t, a_t)}{p_{\theta'}(s_t, a_t)} A^\theta(s_t, a_t) \nabla \log p_\theta(a_t | s_t) \right] \\
&= E_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \frac{p_\theta(a_t | s_t) p_\theta(s_t)}{p_{\theta'}(a_t | s_t) p_{\theta'}(s_t)} A^{\theta'}(s_t, a_t) \nabla \log p_\theta(a_t | s_t) \right] \\
&= E_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \frac{p_\theta(a_t | s_t)}{p_{\theta'}(a_t | s_t)} A^{\theta'}(s_t, a_t) \nabla \log p_\theta(a_t | s_t) \right]
\end{align*}
∇ R θ = E ( s t , a t ) ∼ π θ [ A θ ( s t , a t ) ∇ log p θ ( a t ∣ s t ) ] = E ( s t , a t ) ∼ π θ ′ [ p θ ′ ( s t , a t ) p θ ( s t , a t ) A θ ( s t , a t ) ∇ log p θ ( a t ∣ s t ) ] = E ( s t , a t ) ∼ π θ ′ [ p θ ′ ( a t ∣ s t ) p θ ′ ( s t ) p θ ( a t ∣ s t ) p θ ( s t ) A θ ′ ( s t , a t ) ∇ log p θ ( a t ∣ s t ) ] = E ( s t , a t ) ∼ π θ ′ [ p θ ′ ( a t ∣ s t ) p θ ( a t ∣ s t ) A θ ′ ( s t , a t ) ∇ log p θ ( a t ∣ s t ) ] 根据 ∇ f ( x ) = f ( x ) ∇ log f ( x ) \scriptsize \nabla f(x) = f(x) \nabla \log f(x) ∇ f ( x ) = f ( x ) ∇ log f ( x )
J θ ′ ( θ ) = E ( s t , a t ) ∼ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ]
\scriptsize J^{\theta'}(θ) = E_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \frac{p_\theta(a_t | s_t)}{p_{θ'}(a_t | s_t)} A^{\theta'}(s_t, a_t) \right]
J θ ′ ( θ ) = E ( s t , a t ) ∼ π θ ′ [ p θ ′ ( a t ∣ s t ) p θ ( a t ∣ s t ) A θ ′ ( s t , a t ) ] 即我们的优化目标是最大化我们目标函数表达式。
上述推导成立的条件是重要性采样 。但是,这里隐含掉了一个问题。让我们继续来讨论一下重要性采样下,两个分布期望和方差的差异。
E x ∼ p [ f ( x ) ] = E x ∼ q [ f ( x ) p ( x ) q ( x ) ]
\scriptsize E_{x \sim p}[f(x)] = E_{x \sim q} \left[ f(x) \frac{p(x)}{q(x)} \right]
E x ∼ p [ f ( x )] = E x ∼ q [ f ( x ) q ( x ) p ( x ) ] 根据重要性采样的定义,两者的期望是一致的。
那么,根据方差公式,V a r [ X ] = E [ X 2 ] − ( E [ X ] ) 2 \scriptsize Var[X] = E[X^2] - (E[X])^2 Va r [ X ] = E [ X 2 ] − ( E [ X ] ) 2 p p p
Var x ∼ p [ f ( x ) ] = E x ∼ p [ f ( x ) 2 ] − ( E x ∼ p [ f ( x ) ] ) 2
\scriptsize \text{Var}_{x \sim p}[f(x)] = E_{x \sim p}\left[f(x)^2\right] - \left(E_{x \sim p}[f(x)]\right)^2
Var x ∼ p [ f ( x )] = E x ∼ p [ f ( x ) 2 ] − ( E x ∼ p [ f ( x )] ) 2 我们再继续计算分布q q q
Var x ∼ q [ f ( x ) p ( x ) q ( x ) ] = E x ∼ q [ ( f ( x ) p ( x ) q ( x ) ) 2 ] − ( E x ∼ q [ f ( x ) p ( x ) q ( x ) ] ) 2 = E x ∼ q [ f ( x ) 2 p ( x ) q ( x ) ] − ( E x ∼ p [ f ( x ) ] ) 2
\scriptsize
\begin{align*}
\text{Var}_{x \sim q} \left[ f(x) \frac{p(x)}{q(x)} \right] &= E_{x \sim q} \left[ \left( f(x) \frac{p(x)}{q(x)} \right)^2 \right] - \left( E_{x \sim q} \left[ f(x) \frac{p(x)}{q(x)} \right] \right)^2 \\
&= E_{x \sim q} \left[ f(x)^2 \textcolor{red}{\frac{p(x)}{q(x)}} \right] - \left( E_{x \sim p}[f(x)] \right)^2
\end{align*}
Var x ∼ q [ f ( x ) q ( x ) p ( x ) ] = E x ∼ q [ ( f ( x ) q ( x ) p ( x ) ) 2 ] − ( E x ∼ q [ f ( x ) q ( x ) p ( x ) ] ) 2 = E x ∼ q [ f ( x ) 2 q ( x ) p ( x ) ] − ( E x ∼ p [ f ( x )] ) 2 我们发现,重要性采样的两个分布,尽管期望是一样的,他们的方差是存在一个比例值 p ( x ) / q ( x ) \scriptsize p(x)/q(x) p ( x ) / q ( x )
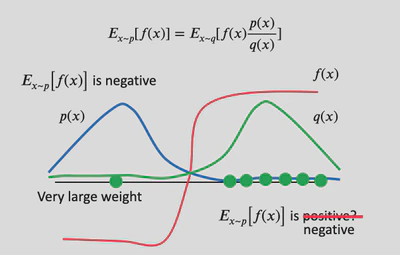
如图所示,p ( x ) , q ( x ) \scriptsize p(x), q(x) p ( x ) , q ( x ) p ( x ) \scriptsize p(x) p ( x ) f ( x ) \scriptsize f(x) f ( x ) f ( x ) \scriptsize f(x) f ( x ) q ( x ) \scriptsize q(x) q ( x ) f ( x ) \scriptsize f(x) f ( x ) q ( x ) \scriptsize q(x) q ( x ) p ( x ) \scriptsize p(x) p ( x ) q ( x ) \scriptsize q(x) q ( x )
答案仍然是,是的。下面将介绍三种递进的解决方法。
TRPO 上文提到我们不希望 θ \scriptsize \theta θ θ ′ \scriptsize \theta' θ ′ δ \scriptsize \delta δ
max θ J TRPO ( θ ′ ) ( θ ) = E ( s t , a t ) ∼ π ( θ ′ ) [ p θ ( a t ∣ s t ) p ( θ ′ ) ( a t ∣ s t ) A ( θ ′ ) ( s t , a t ) ] subject to KL ( θ , θ ′ ) < δ
\scriptsize
\begin{aligned}
& \max_\theta \quad J_{\tiny \text{TRPO}}^{(\theta')}(θ) = E_{(s_t, a_t) \sim \pi_{(\theta')}} \left[ \frac{p_\theta(a_t | s_t)}{p_{(\theta')} (a_t | s_t)} A^{(\theta')} (s_t, a_t) \right] \\
& \text{subject to} \quad \text{KL}(\theta, \theta') < \delta
\end{aligned}
θ max J TRPO ( θ ′ ) ( θ ) = E ( s t , a t ) ∼ π ( θ ′ ) [ p ( θ ′ ) ( a t ∣ s t ) p θ ( a t ∣ s t ) A ( θ ′ ) ( s t , a t ) ] subject to KL ( θ , θ ′ ) < δ 具体证明过程,请详见TRPO论文[18]。
PPO1 实际上,直接求解TRPO这种带约束的问题是十分复杂的,需要计算二阶梯度。Proximal Policy Optimization (PPO)[16]直接把KL散度作为一个惩罚项放到目标函数中。即得到我们的优化目标
J PPO1 θ ′ ( θ ) = E ( s t , a t ) ∼ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ] − β KL ( θ , θ ′ )
\scriptsize
J_{\text{PPO1}}^{\theta'} (\theta) = E_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \frac{p_\theta(a_t | s_t)}{p_{\theta'} (a_t | s_t)} A^{\theta'} (s_t, a_t) \right] - \textcolor{red}{\beta \text{KL}(\theta, \theta')}
J PPO1 θ ′ ( θ ) = E ( s t , a t ) ∼ π θ ′ [ p θ ′ ( a t ∣ s t ) p θ ( a t ∣ s t ) A θ ′ ( s t , a t ) ] − β KL ( θ , θ ′ ) 为了更进一步提高惩罚项的作用,论文加入自适应的思想,当两者分布KL散度较大的时候,增大惩罚,使策略更新更加谨慎;当两个分布较相似的时候,减少惩罚,使之学得更快。即
{ If KL ( θ , θ ′ ) > KL max , increase β If KL ( θ , θ ′ ) < KL min , decrease β
\scriptsize
\begin{cases}
\text{If} \quad \text{KL}(\theta, \theta') > \text{KL}_{\max}, \quad \text{increase} \ \beta \\
\text{If} \quad \text{KL}(\theta, \theta') < \text{KL}_{\min}, \quad \text{decrease} \ \beta
\end{cases}
{ If KL ( θ , θ ′ ) > KL m a x , increase β If KL ( θ , θ ′ ) < KL m i n , decrease β PPO2 PPO2再次提出更简洁的改进方法来限制 θ \scriptsize \theta θ θ ′ \scriptsize \theta' θ ′ ϵ \scriptsize \epsilon ϵ [ 1 − ϵ , 1 + ϵ ] \scriptsize \left[ 1 - \epsilon, 1+ \epsilon \right] [ 1 − ϵ , 1 + ϵ ]
J PPO2 ( θ ) = E ( s t , a t ) ∼ π θ ′ [ min ( r t ( θ ) A θ ′ ( s t , a t ) , clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A θ ′ ( s t , a t ) ) ]
\scriptsize
\begin{align*}
J_{\text{PPO2}} (\theta) = \mathbb{E}_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \min \left( r_t(\theta) A^{\theta'}(s_t, a_t), \\
\text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) A^{\theta'}(s_t, a_t) \right) \right]
\end{align*}
J PPO2 ( θ ) = E ( s t , a t ) ∼ π θ ′ [ min ( r t ( θ ) A θ ′ ( s t , a t ) , clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A θ ′ ( s t , a t ) ) ] 其中,r t ( θ ) = π θ ( a t ∣ s t ) π θ ′ ( a t ∣ s t ) \scriptsize r_t(\theta) = \frac{\pi_\theta(a_t | s_t)}{\pi_{\theta'}(a_t | s_t)} r t ( θ ) = π θ ′ ( a t ∣ s t ) π θ ( a t ∣ s t ) A θ ′ ( s t , a t ) \scriptsize A^{\theta'}(s_t, a_t) A θ ′ ( s t , a t ) p θ \scriptsize p_\theta p θ p θ \scriptsize p_\theta p θ p θ ′ \scriptsize p_\theta' p θ ′
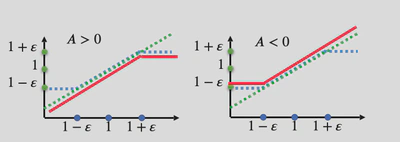
图示中的x轴是 r t ( θ ) \scriptsize r_t(\theta) r t ( θ ) clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) \scriptsize \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) r t ( θ ) \scriptsize r_t(\theta) r t ( θ ) clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) \scriptsize \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) J PPO2 ( θ ) \scriptsize J_{\text{PPO2}} (\theta) J PPO2 ( θ )
PPO完整的算法,继续增加两个小tips,来提高PPO算法的鲁棒性。
J t CLIP+VF+S ( θ ) = E [ J PPO2 θ k ( θ ) − c 1 L t VF ( θ ) + c 2 S [ π θ ] ( s t ) ]
\scriptsize
J_t^{\text{CLIP+VF+S}}(\theta) = \mathbb{E} \left[ J_{\text{PPO2}}^{\theta^k} (\theta) - c_1 L_t^{\text{VF}} (\theta) + c_2 S[\pi_\theta](s_t) \right]
J t CLIP+VF+S ( θ ) = E [ J PPO2 θ k ( θ ) − c 1 L t VF ( θ ) + c 2 S [ π θ ] ( s t ) ] J PPO2 θ k ( θ ) \scriptsize J_{\text{PPO2}}^{\theta^k} (\theta) J PPO2 θ k ( θ ) L t V F ( θ ) = ( V θ ( s t ) − V t t a r g e t ) 2 \scriptsize L_t^{VF} (\theta) = (V_\theta (s_t) - V_t^{target})^2 L t V F ( θ ) = ( V θ ( s t ) − V t t a r g e t ) 2 S [ π θ ] ( s t ) \scriptsize S[\pi_\theta](s_t) S [ π θ ] ( s t )
以上即为PPO方法。
IMPALA DeepMind于2018年发布importance-weighted actor-learner architecture (IMPALA[19]),与其说是一种算法,不如说更像一种分布式训练的Agent架构,论文作者提供了一个优化版实现。
如前所述,A3C的Actor需要周期性的暂停探索,来与中央的参数服务器进行策略权重参数的同步。
IMPALA中的多个Actor同样以并行方式运行,但是它们只负责收集经验,并将这些经验传递到中心的Learner;Learner会负责计算梯度。这里可以说明Actor是不需要暂停,等待模型的同步操作的,即Actor和Learner是完全独立的。
为了有效利用扩展计算资源,IMPALA在配置中可支持单个learner机器,也可支持多个相互之间同步的Learner机器。以这种方式将学习和操作分开也有利于提升整个系统的吞吐量。
然而,这种去耦合的操作,会导致Actor的策略落后于Learner。
为弥补这个滞后,论文提出一种新的 off-policy actor-critic方法,称之为V-trace[19]。
V-trace的目的是根据行为策略 μ \scriptsize \mu μ ( x t , a t , r t ) t = s t = s + n \scriptsize (x_t,a_t,r_t )_{t=s}^{t=s+n} ( x t , a t , r t ) t = s t = s + n v s \scriptsize v_s v s
v s = def V ( x s ) + ∑ t = s s + n − 1 γ t − s ( ∏ i = s t − 1 c i ) δ t V
\scriptsize
v_s \stackrel{\text{def}}{=} V(x_s) + \sum_{t=s}^{s+n-1} \gamma^{t-s} \left( \prod_{i=s}^{t-1} c_i \right) \delta_t V
v s = def V ( x s ) + t = s ∑ s + n − 1 γ t − s ( i = s ∏ t − 1 c i ) δ t V 其中,时刻t \scriptsize t t δ t V = def ρ t ( r t + γ V ( x t + 1 ) − V ( x t ) ) \scriptsize \delta_t V \stackrel{\text{def}}{=} \rho_t (r_t + \gamma V(x_{t+1}) - V(x_t)) δ t V = def ρ t ( r t + γV ( x t + 1 ) − V ( x t )) ρ t = def min ( ρ ˉ , π ( a t ∣ x t ) μ ( a t ∣ x t ) ) \scriptsize \rho_t \stackrel{\text{def}}{=} \min (\bar{\rho}, \frac{\pi(a_t \mid x_t)}{\mu(a_t \mid x_t)}) ρ t = def min ( ρ ˉ , μ ( a t ∣ x t ) π ( a t ∣ x t ) ) c i = def min ( c ˉ , π ( a i ∣ x i ) μ ( a i ∣ x i ) ) \scriptsize c_i \stackrel{\text{def}}{=} \min (\bar{c}, \frac{\pi(a_i \mid x_i)}{\mu(a_i \mid x_i)}) c i = def min ( c ˉ , μ ( a i ∣ x i ) π ( a i ∣ x i ) )
第一个ρ t \scriptsize \rho_t ρ t ∏ i = s t − 1 c i \scriptsize \prod_{i=s}^{t-1} c_i ∏ i = s t − 1 c i
IMPALA使用Actor-Critic的架构更新策略。Critic的更新方式是最小化拟合价值函数 V θ ( x s ) V_\theta (x_s) V θ ( x s ) v s \scriptsize v_s v s
( v s − V θ ( x s ) ) ∇ θ V θ ( x s )
\scriptsize
(v_s - V_\theta (x_s)) \nabla_\theta V_\theta (x_s)
( v s − V θ ( x s )) ∇ θ V θ ( x s ) 根据推导的重要性采样法则下的策略梯度的目标函数,通过行为策略 μ \scriptsize \mu μ π θ \scriptsize \pi_\theta π θ
∇ θ J μ ( θ ) = E μ [ π θ ( a ∣ s ) μ ( a ∣ s ) Q π ( x s , a s ) ∇ θ log π θ ( a ) ]
\scriptsize
\nabla_\theta J_\mu (\theta) = \mathbb{E}_\mu \left[ \frac{\pi_\theta (a \mid s)}{\mu(a \mid s)} Q^\pi (x_s, a_s) \nabla_\theta \log \pi_\theta(a) \right]
∇ θ J μ ( θ ) = E μ [ μ ( a ∣ s ) π θ ( a ∣ s ) Q π ( x s , a s ) ∇ θ log π θ ( a ) ] 使用TD error, r s + γ v s + 1 − V θ ( x s ) \scriptsize r_s + \gamma v_{s+1} - V_\theta (x_s) r s + γ v s + 1 − V θ ( x s ) Q π ( x s , a s ) \scriptsize Q^\pi (x_s, a_s) Q π ( x s , a s ) Q \scriptsize Q Q
∇ θ J μ ( θ ) ≈ E μ [ ρ s ( r s + γ V ( x s + 1 ) − V ( x s ) ) ∇ θ log π θ ( a ) ]
\scriptsize
\nabla_\theta J_\mu (\theta) \approx \mathbb{E}_\mu \left[ \rho_s (r_s + \gamma V(x_{s+1}) - V(x_s)) \nabla_\theta \log \pi_\theta(a) \right]
∇ θ J μ ( θ ) ≈ E μ [ ρ s ( r s + γV ( x s + 1 ) − V ( x s )) ∇ θ log π θ ( a ) ] 那么Actor的梯度更新方向为
ρ s ∇ w log π w ( a s ∣ x s ) ( r s + γ v s + 1 − V θ ( x s ) )
\scriptsize
\rho_s \nabla_w \log \pi_w (a_s \mid x_s) (r_s + \gamma v_{s+1} - V_\theta (x_s))
ρ s ∇ w log π w ( a s ∣ x s ) ( r s + γ v s + 1 − V θ ( x s )) 最后,为了避免提前收敛,加入熵的激励
− ∇ w ∑ a π w ( a ∣ x s ) log π w ( a ∣ x s )
\scriptsize
-\nabla_w \sum_a \pi_w (a \mid x_s) \log \pi_w (a \mid x_s)
− ∇ w a ∑ π w ( a ∣ x s ) log π w ( a ∣ x s ) 基于上面描述的三个参数更新方式,即得到IMPALA算法。从论文实验结果,与A3C方法相比,它的学习效率更高,并且可以处理多出一到两个数量级的经验样本。IMPALA的数据吞吐量也呈现线性增长,表明分布式架构和V-trace算法可以为实现处理大规模强化学习问题提供了一种新的可能性。
Reference [1] Sutton R S, Barto A G. Reinforcement learning: An introduction[M]. [2] policy gradient blog, https://jonathan-hui.medium.com/rl-policy-gradients-explained-9b13b688b146 [3] policy gradient from cs294-112, http://rail.eecs.berkeley.edu/deeprlcourse-fa17/f17docs/lecture_4_policy_gradient.pdf [4] https://www.davidsilver.uk/wp-content/uploads/2020/03/pg.pdf [5] “强化学习(十三) 策略梯度(Policy Gradient) - 刘建平Pinard - 博客园.” [Online]. Available: https://www.cnblogs.com/pinard/p/10137696.html . - [Accessed: 23-May-2019]. [6] R. Sutton, D. Mcallester, S. Singh, and Y. Mansour, “Policy Gradient Methods for Reinforcement Learning with Function Approximation,” - Adv Neural Inf Process Syst, vol. 12, Feb. 2000. [7] 郭宪 and 方勇纯, 深入浅出强化学习:原理入门. 电子工业出版社, 2018. [8] “Hung-yi Lee.” [Online]. Available: http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS18.html . [Accessed: 20-May-2019]. [9] “OpenAI Baselines: ACKTR & A2C,” OpenAI, 18-Aug-2017. [Online]. Available: https://openai.com/blog/baselines-acktr-a2c/ . [Accessed: - 03-Jun-2019]. [10] A. Juliani, “Simple Reinforcement Learning with Tensorflow Part 8: Asynchronous Actor-Critic Agents (A3C),” Medium, 17-Dec-2016. . [11] V. Mnih et al., “Asynchronous Methods for Deep Reinforcement Learning,” Feb. 2016. [12] “mniha16-supp.pdf.” . [13] D. Silver, G. Lever, N. Heess, T. Degris, D. Wierstra, and M. Riedmiller, “Deterministic Policy Gradient Algorithms,” Jun. 2014. [14] “Policy Gradient Algorithms.” [Online]. Available: https://lilianweng.github.io/lil-log/2018/04/08/policy-gradient-algorithms.html#dpg . - [Accessed: 04-Jun-2019]. [15] T. P. Lillicrap et al., “Continuous control with deep reinforcement learning,” Sep. 2015. [16] J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal Policy Optimization Algorithms,” Jul. 2017. [17] “Proximal Policy Optimization,” OpenAI, 20-Jul-2017. [Online]. Available: https://openai.com/blog/openai-baselines-ppo/ . [Accessed: - 04-Jun-2019]. [18] J. Schulman, S. Levine, P. Moritz, M. I. Jordan, and P. Abbeel, “Trust Region Policy Optimization,” Feb. 2015. [19] L. Espeholt et al., “IMPALA: Scalable Distributed Deep-RL with Importance Weighted Actor-Learner Architectures,” Feb. 2018.  xwell.xia from imxwell.com
xwell.xia from imxwell.com