强化学习基本问题回顾总结

Apr 13, 2019·
夏 伟
夏 伟

强化学习问题的概述，从问题定义，到分类，以及传统强化学习算法（主要覆盖DQN之前的RL经典算法,包括：动态规划、蒙特卡洛、时序差分q-learning和sarsa 等）。

RL问题回顾

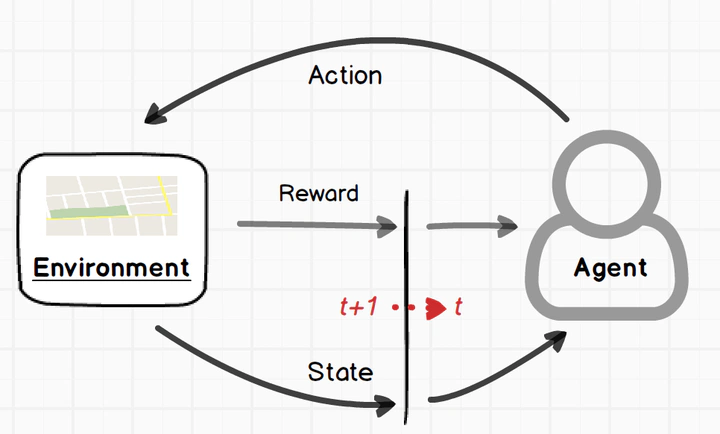
强化学习（Reinforcement Learning）本身可以定义为一个广泛的学习问题，学会找到状态（Situation）到动作（Actions）的一个映射关系，以最大化一个数值型的回报（Reward）信号。一个完整的强化学习问题可以用马氏决策过程中的最优控制理论来进行描述。在马氏链中，当前时刻的状态（State） 仅仅与上一时刻的状态有关。如开篇图所示，一个智能体（Agent）可以通过某种方式感受环境的状态（State），然后可以通过某一个动作（Action）来改变环境的下一状态。在这个不断交互的过程中，Agent还必须具有一个或者以上的、与此环境状态相关的目标（Goal）。可以形式为，强化学习的优化目标是通过选择策略 $\scriptsize \pi$ 来最大化累积奖励 $\scriptsize G_t$，通常对于每一个状态 $\scriptsize s$，表示为：

$$ \scriptsize \max_{\pi} \mathbb{E}_{\pi} \left[ \sum_{t=0}^{\infty} \gamma^t R_{t+1} \mid S_0 = s \right] $$

与RL问题相对应的任何求解方法，可以称之为一个强化学习方法。

1. RL的两个重要特征

  • 试错搜索（trial-and-error）
  • 延迟回报（delayed reward）

可以引出与监督学习的重要区别——评价的方式不同。 监督学习中通过正确的指示（instruct, or label）来进行反馈；强化学习是依靠整个生命周期所选择的动作来进行评价式的反馈。

2. RL系统中的四大主要元素（element）

  • 策略（Policy）

定义某个时刻agent的行为，可以看做策略的映射$\pi_(s_t)$。粗略地说，一个策略可以看做是接收到状态到智能体做出动作的一种映射关系，可以用函数或者表的形式来表现。通常来说，策略可以是确定的，也可能是随机的，即可以用条件概率来表示。

  • 奖励/回报函数（Reward function）

奖励函数定义了强化学习问题中的目标。它把当前每个状态（或者状态-动作对）映射到一个评价数值，以表现该Agent当前所做事件的好坏程度。

  • 值函数（Value function）

奖励函数所表现出的是当前状态或者状态-动作对的立即评价，值函数表征的是对长远意义下的评判。 $V_s$表示当前状态$s$下的累积回报；$V_{(s,a)}$表示当前状态$s$下，执行动作$a$下的累积回报。

粗略来说，值函数可以表示从当前状态开始到未来（long-term），Agent可以收获到奖励的一种累积和。即值函数是对Agent整个生命周期的一种评价。值函数是动作选择的一个标准。

  • 环境的模型（model of the environment）

即对该Agent生存环境的行为模仿（mimics the behavior of the environment）。举一个例子，给定一个状态和动作，环境模型可以预测相对应的下一状态和奖励。如果模型已知，强化学习问题可以演化为动态规划问题求解。

3. RL中智能体学习方法的分类

根据强化学习问题中所含元素的种类，其Agent的学习方法，可以分为5大类。

  • Model-free
  • Model-based
  • Actor-critic (Policy + Value function)
  • Policy-based
  • Value-based

基于值函数的学习方法，一般是去学习一个值函数，来表征状态、状态-动作的好坏情况，这也意味着我们不需要知道策略函数；基于策略的学习方法则是去学习一个策略，比如状态到动作的映射关系；如果我们的算法在学习过程中，同时学习策略和值函数，我们称之为行动者（演员）-评论者（Actor-Critic）方法。策略函数类比一个演员专门负责执行动作，而值函数等同一个评论者，专门负责进行反馈，两者互相促进，以达到学习优化的目标。

根据学习过程中是否学习环境的model信息的这一个维度，又将智能体的学习区分为model-free 和model-based方法。这也意味着，是否基于model对智能体来说，它都可以具备策略、值函数，或者两者均有。

由于具备MDP的相关知识（转移矩阵，reward etc.）, Model-based方法与model-free方法相比，优势是可以通过监督学习的方法来训练一个环境模型，可以对环境模型的不确定性进行推断，从结果来看，model-based对数据样本的使用率往往更高，带来的收益是训练的收敛性也会更好。其缺点是通过学习环境的一个模型，然后再构造一个价值函数（value function），会引入两个近似误差源（two sources of approximation error）。一般来说，可以学习模型包括表查找、线性高斯、深度置信网络等模型架构。

根据不同的学习机制，强化学习过程中仍需重点关注的几组对比概念。

  • On-policy and off-policy：其判断的标准是学习更新（目标）和决策使用（行为）的策略是否为同一个。这两种学习方法，在使用数据更新（backup）策略/值函数的时间点也是不同的。on-policy方法由于更新的策略函数是当前用来执行动作的函数，存在先后依赖的关系，故训练过程中数据的使用会被“串行化”。off-policy是可以独立的两个函数，故可以通过一些机制，如replay buffer，来实现交互历史数据的生成和策略的训练并行化。

  • Exploration and Exploitation：学习算法探索未知的策略，进而完善；还是使用当前最优的策略。这两个步骤是相互矛盾的操作，需要考虑如何调整，来促进整个策略的学习过程。

    • Trade-off between exploration and exploitation. Agent 需要根据已知的状态、动作和回报的相关信息，来不断获得最大的回报，即利用（exploit）当前已知的知识；另外，Agent 需要探索（explore）一些未知的知识，以期望在未来实现更好的动作。（由于目前的知识往往并不是最优的）。因此，在RL中，利用与探索是一个权衡的话题，目前已提出多种方法来尝试解决这个问题。

    • ϵ-greedy action selection（以小概率不贪心的选择方式）

    • Softmax action selection（基于Gibbs分布或者称之为玻尔兹曼分布，以概率选择动作）

      $$\scriptsize \cfrac{e^{Q_t(a)/\tau}}{\sum_{b=1}^n e^{Q_t(b)/\tau}} $$

      τ>0表示温度（temperature）, 高的温度，选择动作近乎平等；温度趋近0的时候，此法接近于贪心选择。

  • Learning and planning：智能体通过与环境直接交互的经验（trajectory/ trail）来Learning，找到一个策略；同时智能体可以利用已有的环境模型进行planning（E.g. 动态规划）

  • Prediction and Control：预测是对未来的评估，即给出一个状态/状态-动作值函数，或者策略；而控制是找到最优的状态/状态-动作值函数，或者策略。

另外，在论文中，经常会出现trajectory，rollout，trial， episode等概念，他们的区别在于：

  • episode （有始有终， 有initial state and terminal state）
  • episodic 是具备有限时间点的事件， 有terminal 状态，进入这个状态后，去其他状态的概率为0；
  • 与episodic想对应的概念，continuous tasks 永远没有结束点。比如，学生在网上学习数学这件事件。
  • 如果是情节式的任务，Episodes 也称之为“trials”。这两个是最接近的概念[4].
  • trajectory，表示(s,a,r) 这样的序列对， 可能来自于采样，具备随机性， 可能是人为构建的序列对，即该序列对可能不会在实际场景中出现的。
  • rollout 是episode 的一个片段， 介于episode 和 trajectory之间的一个概念。 从某个位置开始（非initial），到 terminal 结束。

4. RL与其他机器学习算法的差异

强化学习中的Agent需要与环境持续交互，且需要实时给出action的特性，决定了它与其他的机器学习方法存在较大差异，其主要体现在样本数据的使用和模型在生产环境部署两个方面。

从数据样本的使用角度来看，与监督学习相比，RL没有直接对应的标签值，RL在给出action之后，环境会反馈带有延迟性质的reward，RL优化目标是最大化累积的折扣回报，而监督学习预测的是对应标签值；从无监督学习或者自监督学习的角度看，无监督学习是从大量的数据样本中，尝试找到某种内在的属性或特征；借用LeCun 的例子，把机器学习方法类比水果蛋糕。RL使用的数据仅仅是蛋糕的一颗樱桃；监督学习使用的数据是蛋糕的外表糖衣；而无监督学习看到的是整个蛋糕本身。

5. 传统强化学习算法

5.1 Dynamic Programming

动态规划算法是解决复杂问题的一个经典方法，基于完整的知识假设，算法通过把复杂问题分解为多个子问题，通过求解子问题进而得到整个问题的解。在解决子问题的时候，其结果通常可以存储起来，用作解决后续的复杂问题。

当某个问题具有以下两个特性时，通常可以考虑使用动态规划来求解：1）状态满足最优化原理和无后效性，同时该问题的最优解由数个小问题的最优解构成，可以通过寻找子问题的最优解来得到复杂问题的最优解；2）子问题在复杂问题内重复出现，使得子问题的解，可以被存储起来重复利用。马尔科夫决策过程（MDP）满足上述两个属性.

  1. Bellman方程把问题递归为求解子问题，状态转移矩阵和奖励函数满足无后效性，即当前状态只与上一状态有关，与未来状态无关。

  • 状态值函数的bellman 方程

    $$ \scriptsize v_\pi(s) = \sum_{a \in A} \pi(a \mid s) \left( R_s^a + \gamma \sum_{s' \in S} P(s' \mid s, a) v_\pi(s') \right) $$

  • 状态-动作值函数的bellman方程

    $$ \scriptsize Q_\pi(s, a) = R_s^a + \gamma \sum_{s' \in S} P(s' \mid s, a) \sum_{a' \in A} \pi(a' \mid s') Q_\pi(s', a') $$

  1. 价值函数就相当于存储了一些子问题的解，可以复用。因此可以使用动态规划来求解MDP。 我们可以用动态规划算法来求解一类planning问题。Planning指的是在已知MDP所处环境完美知识的基础上求解最优策略，model结构的知识包括：状态行为空间、转换矩阵、奖励等。

  2. 预测问题可以形式化为: 给定一个 $\scriptsize MDP \left\langle S, A, P, R, \gamma \right\rangle$ 和策略 $\pi$，或者给定一个$\scriptsize MRP \left\langle S, P^{\pi}, R^{\pi}, \gamma \right\rangle$，要求输出基于当前策略$\pi$的价值函数 $V_{\pi}$。控制问题可以形式为：给定一个$\scriptsize MDP \left\langle S,A,P,R,\gamma \right\rangle$ ，要求确定最优价值函数 $V_*$ 和最优策略$\pi_*$。

  3. 这类问题是典型的强化学习问题，我们可以用规划来进行预测和控制。预测问题可以通过策略评估来解决，即在给定策略条件下，迭代计算价值函数；而控制问题可以通过策略/价值迭代来寻找最优策略，先在给定或随机策略下计算状态价值函数，根据状态函数贪婪更新策略，多次反复，直至找到最优策略。

5.2 Monte Carlo Methods

蒙特卡洛(Monte Carlo，MC)方法，也称统计模拟方法，于1940年代中期，随着科学技术的发展和电子计算机的发明，而提出的一种以概率统计理论为指导的数值计算方法。是使用随机数（或更常见的伪随机数）来解决很多计算问题的一系列方法总称。

比如，用随机比赛的方式来评价某一步围棋落子的例子。从需要评价的那一步开始，双方随机落子，直到一局比赛结束。为了保证结果的准确性，这样的随机对局通常需要重复多次，记录下每一盘的结果，最后取这些结果的平均，即可得到这步走棋的一个评价值。最后要做的就是，取这些评价值中最高的一步落子作为接下来的落子。和使用了大量围棋知识的传统方法相比，这种方法几乎不需要围棋的专业知识，只需通过大量随机对局的经验数据就能估计出一步棋的价值。其缺点是，多次对局模拟的计算成本往往较大。

粗略来说，MC是指在不清楚MDP状态转移概率和立即回报的情况下，直接从经历完整的Episode（要求所有的episode都能到达终止态，terminate state）来学习状态价值，通常情况下某状态的价值等于在多个Episode中以进入该状态得到的所有收获的平均值（averaging sample returns）。 另一个使用蒙特卡罗方法估算π值的例子。放置30000个随机点后,$\pi$的估算值与真实值相差$0.07\%$. （计算方式：$\scriptsize (πR^2)/(4R^2)$ 。）

蒙特卡洛树搜索(Monte Carlo tree search，MCTS，wiki)是一种用于某些决策过程的启发式搜索算法，这类算法主要是应用蒙特卡洛方法在游戏树中进行搜索。它基于树数据结构、能权衡探索与利用、在搜索空间巨大时仍有效的搜索算法。

蒙特卡洛树搜索的每个循环包括四个步骤：

  • 选择（Selection）：从根节点R开始，选择连续的子节点向下至叶子节点L。其目标是让游戏树向最优的方向扩展，这是MCTS的精要所在。
  • 扩展（Expansion）：除非任意一方的输赢使得游戏在L结束，否则创建一个或多个子节点并选取其中一个节点C。
  • 仿真（Simulation）：在从节点C开始，用随机策略进行游戏，又称为playout或者rollout。
  • 反向传播（Back propagation）：使用随机游戏的结果，更新从C到R的路径上的节点信息。

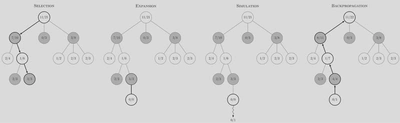
screen reader text
Step of Monte Carlo tree search from Wiki.

每一个节点的内容代表胜利次数/游戏次数 如上图所示，首先已有一定量的节点被加入到树中，从根节点开始,(如根据UCB的值)逐层往下选择的node（如图中的12/21, 7/10, 1/6, 3/3），直到遇到叶子节点(leaf node，图中的3/3)，为该节点添加子节点（图中的0/0），随后从此节点开始进行仿真，得到结果并按照搜索下来的路径将结果返回（注意这里的结果和纯蒙特卡洛方法并不一样，只记录胜负结果而不是子数，胜返回1，负则返回0），然后更新该路径上的每一个节点；在到达结束条件之前，这些操作会一直循环进行下去。可以注意到MCTS是逐步构建搜索树的，并且树是非平衡发展的，更优的node有可能被搜索的更深。

5.3 Temporal-Difference Learning

时序差分（Temporal-Difference，TD）算法结合了前面讲到的动态规划和蒙特卡洛算法。如蒙特卡洛算法一样，它不需要知道具体的环境模型，可以直接从经验中学习；另一方面，继承了DP算法的自举（bootstrap）方法，可以利用学到的估计值来更新，而不用等到一个episode结束后再更新。

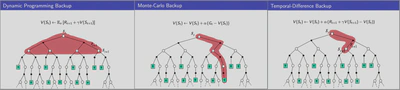
screen reader text

TD算法和MC算法都是基于经验去解决预测问题，给出一些基于策略 π 的样本估计状态 S_t下的值函数 v_π。MC算法是等到一个episode结束得到return以后再借此更新值函数 V(S_t) ，如上图第一列所示。

相较于MC算法，TD算法不需要等到episode最后才能更新值函数，而是一个time step就可以更新一次，如上图中间列所示。因为有可能一个episode会花很长时间，比如玩一个游戏，需要几个小时才能结束一个回合，那么几个小时才能得到一个回报，进行算法的一次训练。换言之，与TD相比，MC算法训练成本更高。

DP算法假设已知MDP过程的完美知识表示。DP没有采样，根据完整的模型，依靠预估数据更新状态价值函数。 TD、DP和MC这三种算法在解决control问题的时候，都是使用广义的策略迭代找到最优策略，其不同点主要在于prediction问题，即根据当前策略估计值函数。在面对exploration和exploitation的两难时，解决算法又分on-policy和off-policy两类算法。

SARSA

Sarsa是一种on-policy TD算法。我们去学习一个最优的动作-状态值函数而不是状态值函数。它的更新法则是：

$$ \scriptsize Q(S,A) \leftarrow Q(S,A) + \alpha [R + \gamma Q(S', \textcolor{red}{A'}) - Q(S,A)] $$

Q-learning

Q-learning是一种off-policy算法,可以收敛到最优的动作-状态价值函数。 其更新法则为：

$$ \scriptsize Q(S,A) \leftarrow Q(S,A) + \alpha [R + \gamma \max_{\textcolor{red}{a}} Q(S', \textcolor{red}{a}) - Q(S,A)] $$

Q-learning与Sarsa只有一点不同，就是在更新 $S_t$ 的动作值函数的时候需要 $S_{t+1}$ 的动作值函数，那状态 $S_{t+1}$ 下的动作怎么选呢？

Sarsa用的是 ε-greedy 方法，和选择 $S_t$ 下的动作一样；而Q-learning是用的 greedy 方法，和选择 $S_t$ 下的动作不一样，因此称为off-policy。

另外，需要注意的是，大写的$A$表示集合，比如 $A_1$则表示$S_1$下的所有动作，而$a$则表示具体的一个动作，它们之间的关系为：$a \in A_1$。回到更新法则中，我们可以发现$a$都在Q-learning的update公式中，这是因为我们在更新时，人为指定选择具有最大值Q的 $a$，这是具有确定性的事件（Deterministic），即学习更新（目标）和决策使用（行为）的策略不是同一个了。而在Q-learning中与环境互动的环节、在Sarsa中更新Q值的环节，以及sarsa中与环境互动的环节时，动作的选择是随机的 ε-greedy，因此所有动作都有可能被选中，只不过是具有最大值Q的动作被选中的概率大。

Cliff walking的例子

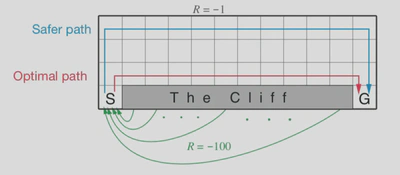
screen reader text

在一个4x12的Grid World中将某些格子设定为悬崖（The Cliff），在设计Reward时，将Agent掉入悬崖的情况记为奖励-100，同时每走一步奖励-1。Cliff Walking问题需要求解的是可以合理避过悬崖到达目标（S->G）的行走策略。

Q-Learning可以收敛出Optimal Polic，而SARSA却选择的是Safer Path，本质上是因为Q-Learning的Target Policy是绝对的greedy策略，绝对的greedy策略保证了Agent在Q值收敛后，不会也不可能再记录可能掉入悬崖的状态动作的Q值，也可以说是Off-Policy类的控制方法并不会受到greedy策略无探索性的影响，所以才能够产生Optimal Policy。

然而, SARSA算法使用的ϵ-greedy 策略来更新Q值，也就是说不论何时，智能体总是有$ϵ$的概率选择非最优的动作，其中掉入悬崖的动作也始终有一定的概率被选中，并在Q函数更新时被记录下来，所以整个Grid的Q函数变成了越靠近悬崖，值越小的分布，最终导致了SARSA选择的是safe path。

Q-Learning的Target Policy是基于Q值的完全greedy policy，但在学习探索过程中决定Agent行走的Behavior Policy的更新却和SARSA同是ϵ-greedy policy。在进入收敛后，由于Q-Learning的Agent每次选择的都是Optimal Path但又因为Behavior Policy保持了一定的探索性，所以总是有一定的概率选择掉入悬崖的动作，虽然这些动作产生的Q值并不会被更新记录。

SARSA的Agent在进入收敛后，基本上选择的是Safe Pass，掉入悬崖的概率比Q-Learning的Agent要小很多。虽然Q-learning学习到了最优策略的价值函数，但其在线表现比SARSA差，因为后者学会了一个迂回政策(roundabout policy)，也就是说，给定$ϵ=0.1$, 在每个episode，Q-learning算法获得的平均reward通常要比SARSA要低。如果随着迭代，$ϵ$逐步衰减的话，最终SARSA和Q-learning 都会收敛到最优策略。

另外，从采样的深度和广度两个维度，整体来看四种算法的差别（增加穷举搜索）。

  • 当使用单个采样，同时不走完整个Episode就是TD；
  • 当使用单个采样但走完整个Episode就是MC；
  • 动态规划DP就是会考虑当前节点全部样本的可能性，但对每一个样本并不走完整个Episode；
  • 那么，如果Agent不但要遍历当前节点的所有Episode，并且把Episode从开始到终止遍历完，就变成了穷举搜索。

5.4 Dyna Q-learning (Integrating Learning and Planning)

Model-based的强化学习方法是指从智能体的经历中，直接学习环境的描述机制，即模型。然后基于该模型进行规划。

当学习价值函数或策略变得很困难的时候，学习模型可能是一条不错的途径，像下棋这类活动，模型是相对直接的，相当于就是游戏规则Model-based RL的优点是：

  1. 可以使用监督式学习方法来获得模型，可进行one-step学习;
  2. 模型能够对个体理解环境提供帮助，通过模型，个体不再局限于如何最大化奖励本身，还能在一定程度上知道采取的动作为什么是好的或者不好，也就是具备一定的推理能力。

当然model-based 的方法也有一些缺点，这是因为在学习模型的过程中，模型其实是一个个体对环境运行机制的描述，不完全是真实环境的运行机制，因此模型会存在一定程度的近似。然后，当使用一个近似的模型去进行价值函数或策略函数的学习时，又会引入一次近似。因此会带来双重的近似误差，有时候这会带来较为严重的错误。因此尽可能要扬长避短。

Model-based RL的能力是来自于近似的 $\scriptsize MDP\left\langle S,A,P_η,R_η\right\rangle$ 中学到的最优策略的。也就是说基于模型的强化学习最好的结果是受到学习到的模型限制，如果模型本身是不准确的，那么Planning过程只能得到一个次优的策略。使用近似的模型解决MDP问题与使用价值函数或策略函数的近似表达来解决MDP问题并不冲突，他们是从不同的角度来近似求解MDP问题，有时候构建一个模型来近似求解MDP比构建一个近似的价值函数或策略函数要更加方便，这是模型的可取之处。同时由于个体经历的更新，模型处在一个动态变化的过程，当利用早期经历构建的模型被后认为存在很大错误，不适用当下经历的时候，需要放弃模型，转而使用不基于模型的强化学习。 那么，把model-base 和model-free的学习结合起来，形成一个整体的架构，利用两者的优点来解决复杂问题。当构建一个环境的模型后，智能体可以有两种经验来源：

  1. 实际经验(real experience): $\scriptsize S' \sim P_{s,s'}^a, \quad R = R_s^a $
  2. 模拟经验(simulated experience): $\scriptsize S' \sim P_{\eta}(S'| S, A), \quad R = R_{\eta}(r|S,A) $

基于这个思想，我们可以把不基于模型的真实经历和基于模型采样得到的模拟经历结合起来，即得到 Dyna 算法。如下图所示，Dyna算法从实际经验中学习得到模型，然后联合使用实际经验和模拟经验一边学习，一边规划更新价值和（或）策略函数。

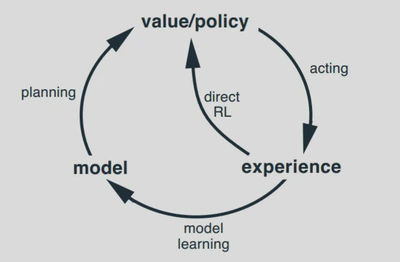
screen reader text

Dyna算法赋予了智能体在与实际环境进行交互式的时候，“独立思考”的能力。即从实际经验中学习，又学习环境模型。 给于智能体一定时间（或次数）的思考。在思考环节，智能体将使用模型，在之前观测过的状态空间中随机采样一个状态，同时从这个状态下，根据曾经使用过的行为中随机选择一个行为，将两者带入模型得到新的状态和奖励，依据这个再次更新行为价值和函数。

RL经典算法对数据/Env使用上的特点

  • 从数据的来源来看，经典RL算法的经验数据，一方面来自智能体与（真实或者虚拟）环境的交互，也可能来自智能体基于环境model的采样评估。从平台化的角度看，数据的来源通道应该是可扩展的，并且与策略的更新应该具备对应关系。

  • 从策略/值函数更新（backup）的时间点来看，支持智能体与环境交互过程的周期不固定，智能体的更新时刻点是可以随意的，同时，在某些时间点智能体的交互可能会扩展更多的交互“分支”。如MCTS，在叶子节点会扩展出更多的子节点进行仿真。

  • 从更新目标策略与行为执行策略是否相同的角度看，主要是区分on-policy 和off-policy。On-policy 从单个智能体的角度看，行动策略的新一步执行，都受限于同一个策略的更新，从单个智能体的角度看，确实是被“串行化”了，在后文中的DRL里面再次分析如何解决该问题；off-policy的目标策略和执行策略是两个，故可以通过独立的线程分开处理。

Reference

强化学习
夏 伟
Authors
夏 伟
Senior Researcher
My research interests include large language model, Reinforcement learning for Recommender System and Automatic (AI) Systems.

Related