深度强化学习方法-DQN系列

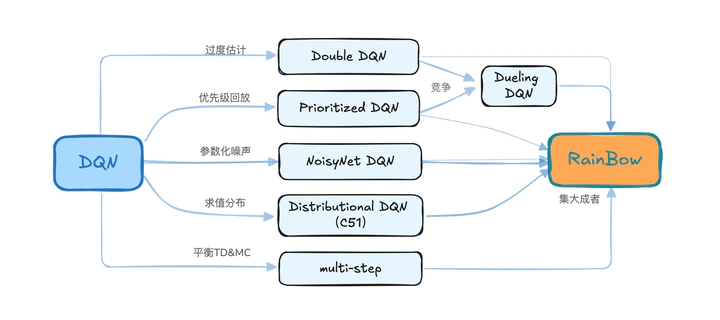
基于dqn 的强化学习方法的梳理总结，从经典的DQN算法开始，总结不同方法的改进策略，到集大成者Rainbow算法。

DQN

DQN算法含两个版本，第一版本于NIPS2013提出[1]，其核心思想是: a）利用深度网络来近似拟合值函数，来解决连续状态空间问题；2）提出experience replay（可以简单理解为一个历史交互数据的buffer，“经验回放池”）的机制来解决数据间的相关性和非静态分布的问题；c）使用经典的Q-learning进行RL问题求解。

用一个深度神经网络来表征 Q 值，参数为 $\theta$ ，

\scriptsize Q(s,a;\theta) = \sum \left[ r + \gamma \max_{a'} Q(s', a';\theta) \right] \approx Q_\pi (s,a)

在Q值中使用均方差mean-square error 来定义目标函数, 使用了Q-Learning要更新的Q值作为目标值。

\scriptsize L(\theta) = \mathbb{E} \left[ \left( \underbrace{r + \gamma \max_{a'} Q(s', a'; \theta)}_{\text{Target}} - Q(s, a; \theta) \right)^2 \right]

3.计算参数 $\theta$ 关于loss function的梯度

\scriptsize \frac{\partial L(\theta)}{\partial \theta} = \mathbb{E} \left[ \left( \underbrace{r + \gamma \max_{a'} Q(s', a'; \theta)}_{\text{Target}} - Q(s, a; \theta) \right) \frac{\partial Q(s, a; \theta)}{\partial \theta} \right]

使用SGD实现End-to-end的优化目标

有了上面的梯度，而 $\scriptsize \frac{\partial Q(s, a; \theta)}{\partial \theta}$ 可以从深度神经网络中进行计算，因此，就可以使用SGD 随机梯度下降来更新参数，从而得到最优的Q值。

根据上面的公式，在梯度更新时，当前的值函数 $Q(s,a;θ)$ 和目标值函数的 $\max_{a'} Q(s', a'; \theta)$ 都是由同一个 Q-network产生的。这样面临一个训练难题，RL交互过程中不同episode 的 state 变化会导致 Q-network 产生的样本呈非静态分布，从而导致训练出的 policy 不稳定。15年的 DQN 版本[2]里，为了解决数据的非静态问题，提出使用两个 Q-network, 并进行周期性同步。

是正常的动作-状态值函数Main Network，输出作为当前值函数，记为 $\hat{Q}(s, a; \textcolor{red}{\theta})$ ；
学习的Target network，输出作为目标值函数，记为 $\hat{Q}(s,a;\textcolor{red}{θ^-})$

至此，解决的范围主要是离散空间的action的问题，即DQN还不能解决连续action空间的问题，以及CNN本身的缺陷不能有效处理长时间的记忆问题。

Double DQN

在DQN算法以及通用的Q-learning算法中，目标Q值都是通过贪婪法直接得到的，即 $\scriptsize Target = r + \gamma \max_{a'} Q(s', a'; \theta)$ 。 $max$ 操作可以让Q值向可能的优化目标快速逼近，但是很容易过犹不及，导致过度估计(Over Estimation)[3]，所谓过度估计就是最终我们得到的算法模型有很大的偏差(bias)。为了解决这个问题， Double Q-Learning, DDQN[4]通过解耦目标Q值下动作的选择和目标 $\hat{Q}$ 值的计算这两步，来达到消除过度估计的问题。

DDQN具体的做法是在DQN的基础上，通过解耦目标Q值下动作的选择和目标Q值的计算这两步，来消除过度估计的问题。

在DQN中，目标Q值得计算方法是： $\scriptsize Target = r + \gamma \max_{a'} Q(s', a'; \theta^-)$ . 在DDQN这里，不再是直接在目标Q网络里面找各个动作中最大的Q值，而是先在当前Q网络中先找出最大Q值对应的动作，即

\scriptsize a^{\text{max}} (s'; \theta) = \arg\max_{a'} Q(s', a'; \theta)

然后利用这个选择出来的动作 $a^{\text{max}} (s'; \theta)$ , 在目标网络里面去计算目标Q值。即：

\scriptsize \text{Target} = r + \gamma \cdot \hat{Q}(s', \textcolor{red}{a^{\text{max}}(s'; \theta)}, \theta^-)

综合起来可以形式化为如下式,区分两个Q值网络： $\theta$ 和 $\theta^-$ ：

\scriptsize \text{Target}_t^{\text{\tiny DDQN}} = r_{t+1} + \gamma \cdot \hat{Q} \left( s_{t+1}, \arg\max_{a'} Q(s_{t+1}, a'; \theta), \theta_t^- \right)

除了目标Q值的计算方式这点以外，DDQN算法和DQN的算法流程完全相同。具体的结果如前面提到的对比图。

Prioritized Experience Replay

在前面的DQN中提到，使用replay buffer机制可以解决数据间的相关性和非静态分布的问题。通过对经验池的数据进行batch采样，进而估计目标Q值。在采样过程中，经验池中的所有样本被采样的概率是一样的。这里会存在一个问题：稀疏reward环境下，memory里面会存储很多无用的数据（reward=0），这样就会采样出很多对训练没有实际作用的样本，最终导致学习的效率很低，甚至学不到策略。于是我们可以从replay buffer 的取用机制上面进行优化？

注意到在经验回放池里面的不同的样本由于TD误差的不同，对network反向传播的作用也应该是不一样的。TD误差越大，那么对我们反向传播的作用越大。而TD误差小的样本，对反向梯度的计算影响也越小。在Q网络中，TD误差就是目标Q网络计算的目标Q值和当前Q网络计算Q值之间的差距。

\scriptsize \text{TD Error} = r + \gamma \max_{a'} Q(s', a'; \theta) - Q(s, a; \theta)

如果完全遵从TD-error越大，重放的概率越大这条原则，也会带来一些样本多样性丧失的问题。比如，

小TD-error的transition $\scriptsize (S_t;A_t;R_{t+1}; \gamma_t; S_{t+1})$ 长时间不能进行回放；
TD-error对噪声很敏感，容易引入噪声的误差估计；
高TD-error的transition被频繁重复回放，进而产生过拟合。

为了解决这些问题，通过控制参数 $\alpha$ ，引入stochastic sampling 的方法， $\scriptsize P(i) = \frac{p_i^\alpha}{\sum_k p_k^\alpha}$ , $p_i > 0$ , 表示第i 个 transition 的优先级，指数 $\alpha$ 用于表示使用多高的优先级(importance sample)，当 $\alpha=0$ 的时候表示所有transition的优先级是一样的。基于这个思想，作者实现两种变体结构，

\scriptsize p_i = | \delta_i | + \epsilon \quad \text{and} \quad p_i = \frac{1}{\text{rank}(i)}

其中， $\epsilon$ 是一个很小的正常数为了使有一些TD-error为0 的特殊边缘例子也能够被抽取；rank(i)是按照 $| \delta_i |$ 排序时transition i的等级。存储结构上使用二进制堆结构（sum-tree）进行存储，可以实现 $O(logN)$ 的更新和采样[5]，作者经过实验，这两种变体都可以加速算法的收敛。

采用优先回放的概率分布采样时，动作值的估计是一个有偏估计。因为采样分布于动作值函数分布完全不同，为了矫正这个偏差，需要乘以一个重要性采样系数,importance-sampling weights, $\scriptsize w_i = \left( \frac{1}{N \cdot P(i)} \right)^\beta$ 来进行弥补。这里当 $\beta=1$ 时，更新效果实际上等同于 Replay Buffer，当 $\beta<1$ 时，优先的经验回放就能够发挥作用了。把经验回放添加优先级的目的就是让更新变得有偏，加入这个纠正是为了说明，可以通过一些设定让它回到普通经验回放一样的更新方式。可以根据实际问题调整权重，即调整 $\beta$ ，让它在两种更新效果之间做一个权衡。比如开始的时候，可以让 $\beta$ 在训练开始时采样系数, $w_i$ 为一个小于1的数，然后随着训练迭代数的增加，让 $\beta$ 不断变大，并最终达到 1。

Dueling DQN

Dueling DQN借鉴Advantage的思想，从网络结构角度来优化DQN算法[6]，与普通DQN的主要差别体现在结构上，如下图所示。

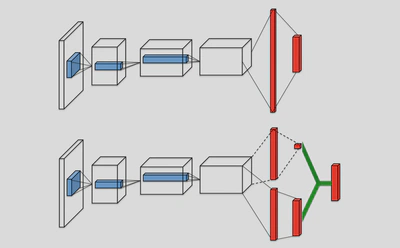
Dueling DQN考虑将Q网络分成两部分，第一部分是仅仅与状态S有关，与具体要采用的动作A无关，这部分叫做状态价值函数部分，记做 $V(S;\theta,\beta)$ ,第二部分同时与状态S和动作A有关，这部分叫做优势函数(Advantage Function)部分,记为 $A(S,A;\theta,\alpha)$ , 最终我们的价值函数可以重新表示为状态价值函数和优势函数的线性组合，即：

\scriptsize Q(S,A;\theta,\alpha,\beta)=V(S;\theta,\beta)+A(S,A;\theta,\alpha)

其中， $\theta$ 是公共部分的网络参数，而 $\beta$ 是状态价值函数独有部分的网络参数，而 $\alpha$ 是优势函数独有部分的网络参数。这样的网络如何train才能达到这种可辨识性质（identifiability）呢？

论文通过限制优势函数状态价值函数的关系来实现竞争，驱使状态价值函数逼近状态动作价值函数。作者提供了两种思路，一种是在状态价值函数上面增加一个常量的同时，在优势函数上去减去这个常量，即

\scriptsize \begin{align*} Q(s,a;\theta,\alpha,\beta) &= V(s;\theta,\beta) \\ &+ \left[ A(s,a;\theta,\alpha) - \max_{a' \in A} A(s,a';\theta,\beta) \right] \end{align*}

当 $a^* = \arg \max_{a' \in A} A(s, a'; \theta, \beta)$ 时， $\arg \max_{a' \in A} Q(s, a; \theta, \alpha, \beta)$ 同时成立，所以此时， $V(s;\theta,\beta)$ 提供个了一个值函数的估计。另外一个更加简便的方法是，我们直接把max 操作替换成平均，即

\scriptsize \begin{align*} Q(s,a;\theta,\alpha,\beta) &= V(s;\theta,\beta) \\ &+ \left[A(s,a;\theta,\alpha) - \frac{1}{|A|} \sum_{a'} A(s,a';\theta,\beta) \right] \end{align*}

经作者验证，限制优势函数期望为零的方法，即 $\scriptsize E_(a \sim \pi(s) ) [A_{(s,a)}]=0$ ，不但使目标函数off化（off-target，联想off-policy），并且由于只需要计算均值，不需要对最优动作进行计算，提高了优化的稳定性。

论文中对上述两个优化函数都进行了测试，获得了类似的结果，由于第二种优化函数的计算更简便，故论文具体的编码测试都是使用后者进行优化。另外，dueling DQN算法，只是改变了网络的内部结构，故可以直接使用DQN的方法进行训练。

Noisy-net DQN

ICLR 2018，OpenAI[8] 和DeepMind[9] 同时分别提出使用Noisy 的方法改进DQN。在每一个episode开始的时候，增加噪声来提高智能体对环境的探索力度。常用的Noise on Action，比如 $\epsilon-greedy$ ,

\scriptsize a = \begin{cases} \arg \max_a Q(s, a) & \text{with probability } 1-\epsilon \\ \text{random} & \text{otherwise} \end{cases}

加在动作上的噪声可能会出现这样的现象：同一状态下，智能体可能会给出不同的动作。在现实的情况中，这种“随机尝试”的策略可能是存在的。作者进而引入状态依赖的探索的观点，State-dependent exploration，在相同（相似）状态下，Agent采取的动作应该是一致的。在每一个episode期间，我们的策略不会被改变，只在每个episode 开始的时候引入噪声参数，保证智能体在一个episode期间的策略是不被扰动的，non-perturbed。即我们应该进行系统地尝试。那么我们可以在Q-function的参数上增加noise，即

\scriptsize a = \arg \max_a \widetilde{Q}(s, a), \quad Q(s, a) \xrightarrow{\text{add noise}} \widetilde{Q}(s, a)

在同样的思路下面，openai 和 deepmind 各给出了一种实现方案

OpenAI直接在Q 函数上面加一个高斯噪声；为提高自适应性，在是否增加扰动噪声两种策略的动作空间KL距离基础上，增加一个自适应的参数，

\scriptsize \widetilde{\pi}(s_t) = \pi(s_t) + N(0, \sigma^2 I) \\ \sigma_{k+1} = \begin{cases} a \sigma_k & \text{if } d(\pi, \widetilde{\pi}) < \delta \\ \frac{1}{a} \sigma_k & \text{otherwise} \end{cases}

2）DeepMind增加一个参数化的NoisyNet，噪声的参数可以根据蒙特卡洛的方法进行更新。我们以p表示输入，q表示输出。参数的形式可以表示如下。

\scriptsize y \stackrel{\text{def}}{=} (\mu^w + \sigma^w \odot \epsilon^w)x + (\mu^b + \sigma^b \odot \epsilon^b)

其中， $\scriptsize \mu^w \in R^{q×p}, \mu^b \in R^q, \sigma^w \in R^{q×p}, \sigma^b \in R^q$ 等参数是需要学习训练的， $\scriptsize \epsilon^w \in R^{q×p}, \epsilon^b \in R^q$ 是表示噪声的随机变量。经实验验证，两种方法都能分别在当时的sota算法，DQN, etc.上面具有reward的明显提升。

Multi-step DQN

Q-learning 方法使用单步的transition的信息进行学习更新Q函数；蒙特卡洛方法需要等到episode 结束后，获取完整的trajectory之后，才能更新Q函数。那么，有没有一个平衡的方法，来兼顾两者呢？Multi-step方法就是使用N次transition的信息对Q函数进行更新学习。那么基于multi-step的DQN变体的目标函数[11]为

\scriptsize \mathbb{L} = \left( \underbrace{r_{t+1}^n + \gamma_t^n \cdot \max_{a'} Q(s_{t+n}, a'; \theta^-)}_{\text{Target}} - Q(s_t, a_t; \theta) \right)^2

C51 (Distributional Q-function)

在RL问题中，智能体与环境之间的交互过程存在随机性，折算的累积回报亦是一个随机变量Z，给定策略π 之后，随机变量Z服从一个分布，我们称之为值分布。经典的RL算法求折算累积回报，就是去优化值分布的均值期望，而忽略了整个分布所具备的信息。同时还会存在一个问题，不同分布的期望也可能是一样。C51算法就是来求解每个action它自己的distribution信息，使用网络来拟合每个动作的分布[10]。

RainBow (DQN 改进集合)

在前面章节里，提到了6种DQN的改进方法，那么我们是否可以把所有的改进方法全部综合在在一起呢？

答案是，RainBow。

实验显示，综合的变体RainBow性能在7百万frame之后，达到最好性能。论文中消融实现显示：依次移除不同方法，均有不同程度影响。有一点值得关注的是移除double之后，并没有性能的明显降低。论文中给的一个解释是：加入 Distribution 之后，由于会对每个action的分布进行估计，故不会出现过度估计的情况。

在一些推荐场景中，在线的强化学习算法可能会对用户和系统带来不可控的影响，故有一些离线强化学习方法开始在推荐场景进行应用，比如BCQ，CQL等。暂不在这里展开。

Reference

[1] V. Mnih et al., “Playing Atari with Deep Reinforcement Learning,” Dec. 2013.
[2] V. Mnih et al., “Human-level control through deep reinforcement learning,” Nature, vol. 518, no. 7540, pp. 529–533, Feb. 2015.
[3]] H. V. Hasselt, “Double Q-learning,” in Advances in Neural Information Processing Systems 23, J. D. Lafferty, C. K. I. Williams, J. - Shaw-Taylor, R. S. Zemel, and A. Culotta, Eds. Curran Associates, Inc., 2010, pp. 2613–2621.
[4] H. van Hasselt, A. Guez, and D. Silver, “Deep Reinforcement Learning with Double Q-Learning,” in Thirtieth AAAI Conference on - Artiicial Intelligence, 2016.
[5] T. Schaul, J. Quan, I. Antonoglou, and D. Silver, “Prioritized Experience Replay,” Nov. 2015.
[6]] Z. Wang, T. Schaul, M. Hessel, H. van Hasselt, M. Lanctot, and N. de Freitas, “Dueling Network Architectures for Deep Reinforcement - Learing,” Nov. 2015.
[7] “Hung-yi Lee.” [Online]. Available: http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS18.html. [Accessed: 20-May-2019].
[8] M. Plappert et al., “Parameter Space Noise for Exploration,” Jun. 2017.
[9] M. Fortunato et al., “Noisy Networks for Exploration,” Jun. 2017.
[10] M. G. Bellemare, W. Dabney, and R. Munos, “A Distributional Perspective on Reinforcement Learning,” Jul. 2017.
[11] Sutton R S, Barto A G. Reinforcement learning: An introduction[M].